leetcode994. 腐烂的橘子
宋标 Lv5
  2022-04-06 19:04:16 2022-04-06 19:04    

题目

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

  • 值 0 代表空单元格；
  • 值 1 代表新鲜橘子；
  • 值 2 代表腐烂的橘子。

每分钟，腐烂的橘子周围 4 个方向上相邻的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例 1：

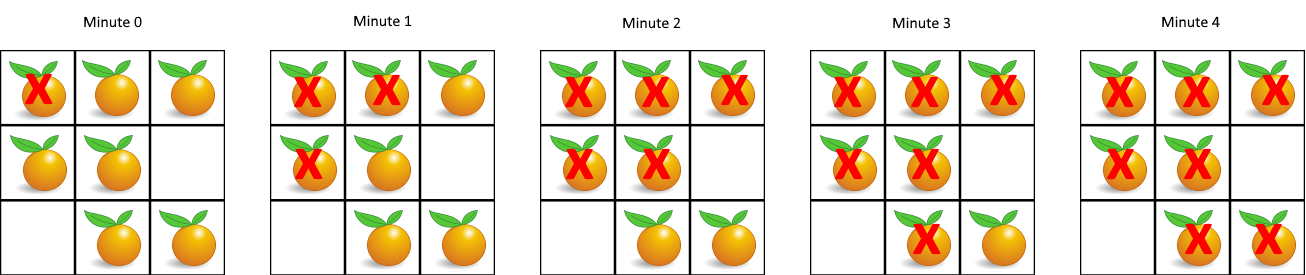
输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4

示例 2：

输入：grid = [[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个正向上。

示例 3：

输入：grid = [[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。  

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 10
  • grid[i][j] 仅为 0、1 或 2

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/rotting-oranges
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题解

注意：
题目中存在多个腐烂橘子(多个源点)，所有腐烂的橘子会同时扩散

思路:

  1. 将所有腐烂橘子看作一个整体,赋一个初始值0，向外扩散。
  2. 被扩散腐烂的橘子消耗的分钟等于扩散点的值+1，依次继续扩散，直到扩散结束。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
class Solution {

    private int[][] xy= {{0,1},{1,0},{-1,0},{0,-1}};

    public int orangesRotting(int[][] grid) {
        LinkedList<int[]> queue = new LinkedList();
        Map<Integer,Integer> depth = new HashMap();
        int m,n;
        int frish = 0;
        m = grid.length;
        n = grid[0].length;
        
        for(int i=0;i<m;++i){
            for(int j=0;j<n;++j){
                int cur = grid[i][j];
                if(cur==2){
                    //初始0分钟
                    depth.put(i*n+j,0);
                    //将所有腐烂的橘子预先加入队列中
                    queue.addFirst(new int[]{i,j});
                }else if(cur==1){
                    //统计所有新鲜的橘子数量
                    ++frish;
                }
            }
        }

        //最后一个腐烂橘子花费的时间
        int ans = 0;
        // 腐烂扩散(广度优先遍历)
        while(!queue.isEmpty()){
            int[] cell = queue.poll();
            int i = cell[0],j = cell[1];
            for(int k=0;k<4;++k){
                int x = i+xy[k][0];
                int y = j+xy[k][1];
                if(x>=0 && x<m && y>=0 && y<n && grid[x][y]==1){
                    grid[x][y]=2;
                    //持续扩散
                    queue.addLast(new int[]{x,y});
                    //花费的分钟等于传播点的值+1
                    ans = depth.get(i*n+j)+1;
                    depth.put(x*n+y,ans);
                    //新鲜橘子数量减1
                    --frish;
                }
                
            }
        }
        //如果还存在新鲜橘子则返回-1
        return frish==0?ans:-1;
    }
}
 评论